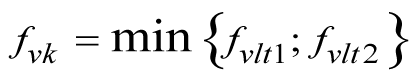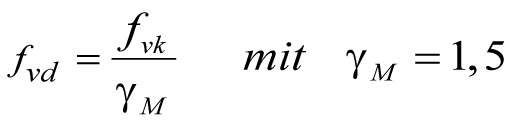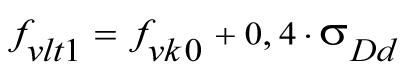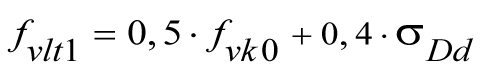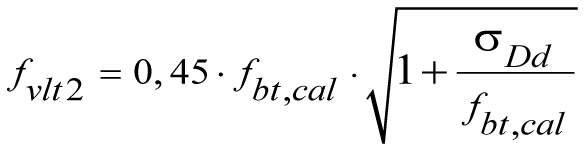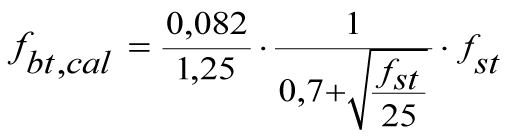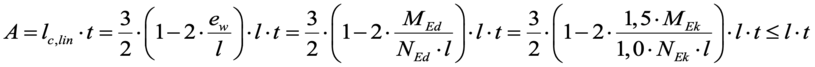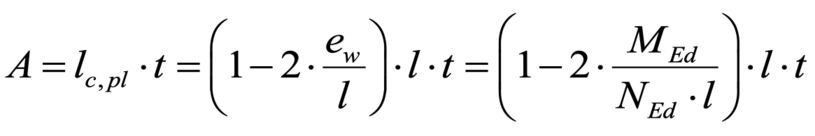8.3.2 Nachweis bei Scheibenschub
8.3.2.2 Charakteristische Schubfestigkeit
Die Schubfestigkeit fvk ist eine wichtige Einflussgröße zur Beurteilung der Querkrafttragfähigkeit von Mauerwerk, die vor allem für den Standsicherheitsnachweis von Aussteifungswänden und Kellerwänden von großer Bedeutung ist. Generell ist dabei wiederum zwischen Scheibenschub- und Plattenschubbeanspruchung zu unterscheiden (s. Kap. 8.1). Die Schubfestigkeit unter Plattenschubbeanspruchung wird in Kapitel 8.3.3.1 behandelt.
Die charakteristische Schubfestigkeit fvk ergibt sich bei Scheibenschub - je nachdem ob Reibungs- oder Steinzugversagen maßgebend wird - aus dem kleineren der beiden Werte für fvlt:
mit
fvlt1 charakteristische Schubfestigkeit im Fall von Reibungsversagen
fvlt2 charakteristische Schubfestigkeit im Fall von Steinzugversagen
Die Schubfestigkeit unter Scheibenbeanspruchung bestimmt sich auf der Grundlage des in [16] entwickelten Versagensmodells für Reibungs- und Steinzugversagen (vgl. Kap. 8.2.1). Der Bemessungswert der Schubfestigkeit fvd ermittelt sich aus dem charakteristischen Wert wie folgt:
Für die Bestimmung der Schubfestigkeit von Mauerwerkswänden nach den Gleichungen (8.4) und (8.5) wird grundsätzlich von einer über die überdrückte Querschnittsfläche gemittelten vorhandenen Normalspannung σDd ausgegangen. Zur Berücksichtigung der ungleichmäßigen Spannungsverteilung in den Lagerfugen wird nach DIN EN 1996-1-1/NA bei Scheibenbeanspruchung ersatzweise ein abgeminderter Reibungsbeiwert von μ‘ = μ/(1 + μ) = 0,4 und eine abgeminderte Haftscherfestigkeit fvk0 angesetzt. Bei größeren Normalspannungen ist zusätzlich ein Versagen der Steine auf Querzug möglich (Gleichung (8.6)).
Reibungsversagen
bei vermörtelten Stoßfugen:
bei unvermörtelten Stoßfugen:
Steinzugversagen
unabhängig von der Ausführung der Stoßfugen:
mit
fvk0 Haftscherfestigkeit nach Tabelle 8-1
fbt,cal Charakteristische Steinzugfestigkeit mit
fbt,cal = 0,020 ∙ fst für Hohlblocksteine
fbt,cal = 0,026 ∙ fst für Hochlochsteine und Steine mit Grifflöchern oder Grifftaschen
fbt,cal = 0,032 ∙ fst für Vollsteine der Höhe ≥ 248mm ohne Grifflöcher oder Grifftaschen
fbt,cal nach Gl. (8.7) für Porenbetonplansteine mit lu ≥ 498 mm und hu ≥ 248 mm
fst umgerechnete mittlere Steindruckfestigkeit nach Tabelle 8-2
σDd Bemessungswert der zugehörigen Druckspannung an der Stelle der maximalen Schubspannung.
Für Rechteckquerschnitte gilt σDd = NEd / A mit A nach Gleichung (8.8)
mit
fst nach Gl. (8.6)
Tabelle 8-1: Haftscherfestigkeit fvk0 von Mauerwerk ohne Auflast nach [8]
| fvk0 [N/mm²] | |||||
| Normalmauermörtel mit einer Festigkeit fm [N/mm²] | Dünnbettmörtel (Lagerfugendicke 1mm bis 3mm) | Leichtmauermörtel | |||
| NM II | NM IIa | NM III | NM IIIa | ||
| 2,5 | 5,0 | 10,0 | 20,0 | ||
| 0,08 | 0,18 | 0,22 | 0,26 | 0,22 | 0,18 |
Tabelle 8-2: Rechenwerte für fst von Mauersteinen nach [8]
| Druckfestigkeitsklasse der Mauersteine und Planelemente | 2 | 4 | 6 | 8 | 10 | 12 | 16 | 20 | 28 | 36 | 48 | 60 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Umgerechnete mittlere Mindestdruckfestigkeit fst [N/mm²] | 2,5 | 5,0 | 7,5 | 10,0 | 12,5 | 15,0 | 20,0 | 25,0 | 35,0 | 45,0 | 60,0 | 75,0 |
Für die Bestimmung der maßgebenden Querschnittsfläche unter Berücksichtigung der überdrückten Wandlänge lc darf aufgrund der für den Querkraftnachweis maßgebenden Einwirkungskombination unter minimaler Normalkraft von linear elastischen Materialverhalten ausgegangen werden. Damit ergibt sich für die überdrückte Querschnittsfläche:
mit
lc,lin überdrückte Wandlänge bei Ansatz einer linear-elastischen Materialverhaltens
t Wanddicke
ew Exzentrizität in Wandlängsrichtung ew = MEd / NEd
MEd maximaler Bemessungswert des einwirkenden Momentes in Wandlängsrichtung
NEd Bemessungswert der einwirkenden Normalkraft. Im Regelfall ist die minimale Einwirkung maßgebend NEd = 1,0 ∙ NGk
NEk charakteristischer Wert der minimalen vertikalen Einwirkung. Im Regelfall NEk = NGk
MEk maximaler charakteristischer Wert des einwirkenden Momentes in Wandlängsrichtung
l Wandlänge
Beim Nachweis gegen Schubdruckversagen unter maximaler Vertikallast ist dagegen von einer starr-plastischen Spannungs-Dehnungs-Beziehung auszugehen und die anzusetzende überdrückte Fläche ergibt sich zu: