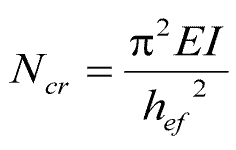Mauerwerkswände sind in den meisten baupraktischen Fällen überwiegend druckbeansprucht, da Mauerwerk diese Art der Belastung am besten abtragen kann (vgl. Kap. 1 und Kap. 2). Bei schlanken Wänden besteht neben dem Versagen durch Überschreiten der Druckfestigkeit (Spannungsversagen) jedoch stets die Gefahr eines Stabilitätsversagens, welches umgangssprachlich häufig als „Ausknicken“ bezeichnet wird. Diese Versagensart ist dadurch gekennzeichnet, dass bei einem überwiegend normalkraftbeanspruchten Bauteil die infolge Lastexzentrizität entstehenden Biegemomente nach Theorie I. und II. Ordnung bei Überschreiten einer kritischen Laststufe schneller anwachsen als die vom Querschnitt mit zunehmender Querschnittsverkrümmung aufnehmbaren Schnittgrößen. Theoretisch steigt bei linear-elastischem Werkstoffverhalten, exakt zentrischer Lasteinleitung und idealgerader Stabachse die aufnehmbare Normalkraft bis zu einem gewissen Wert – der Knicklast – ohne eine Querschnittsverkrümmung an und bei Überschreitung derselben versagt das Bauteil schlagartig. In der Praxis wird die Wand allerdings nie exakt lotrecht ausgeführt und immer mit gewissen Ausmittigkeiten hinsichtlich der Lasteinleitung behaftet sein, sodass bei einwirkender Normalkraft stets Biegemomente nach Theorie I. Ordnung entstehen. Diese wiederum führen zu Zusatzmomenten nach Theorie II. Ordnung, weshalb es sich im Versagensfall - bei Annahme linear-elastischen Werkstoffverhalten - immer um ein Spannungsversagen nach Theorie II. Ordnung handelt. Berücksichtigt man bei der Berechnung der aufnehmbaren Traglast hingegen realitätsnah das infolge Rissbildung in der Wand nichtlineare Last-Verformungs-Verhalten, so kann tatsächlich „echtes“ Stabilitätsversagen auftreten, d.h. der Versagenspunkt liegt innerhalb der maximalen Tragfähigkeitskurve bei Momenten-Normalkraft-Interaktion (s. Bild 5-1).

Im Allgemeinen werden die Schnittgrößen am unverformten System nach Theorie I. Ordnung ermittelt. Beeinflussen die Verformungen jedoch maßgeblich die Schnittkräfte, muss das Gleichgewicht am verformten System nachgewiesen werden. Bei einer druckbelasteten Stütze ergibt sich das Zusatzmoment nach Theorie II. Ordnung aus dem Produkt der Normalkraft und der Verformung. Die Größe der Verformung hängt außer von der Belastung und Geometrie des Systems auch von der Biegesteifigkeit des Stabes ab. Ist die Biegesteifigkeit konstant, kann die Verformung und damit das Zusatzmoment nach der Elastizitätstheorie ermittelt werden. Beim Mauerwerk handelt es sich jedoch um einen nichtlinearen Werkstoff, da sich durch Rissbildung die Steifigkeit des Mauerwerks ändert. Die Rissbildung ist abhängig von der Belastung. Ein Mauerwerksstab mit großer Normalkraft reißt bei einer höheren Momentenbelastung als ein Stab mit geringerer Normalkraft. Das nichtlineare Werkstoffverhalten wird auch als physikalische Nichtlinearität bezeichnet.

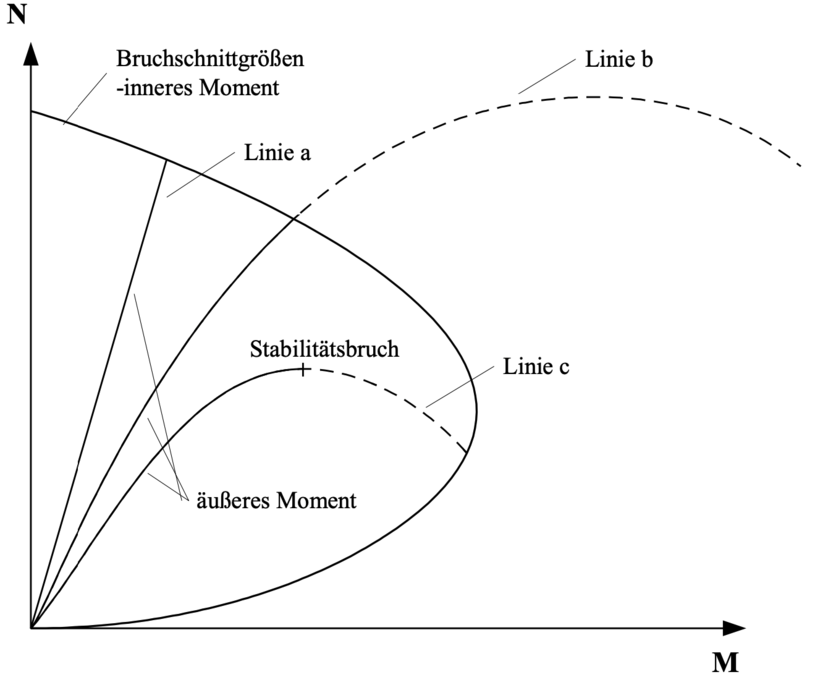
Bei schlanken, druckbeanspruchten Stützen ergeben sich wegen des nichtlinearen Materialverhaltens verschiedene Versagensmöglichkeiten, die sich mithilfe eines Interaktionsdiagramms erläutern lassen. Das Interaktionsdiagramm in Bild 5-1 zeigt die aufnehmbare Normalkraft in Abhängigkeit des Momentes. Erreicht der Stützenquerschnitt die Bruchschnittgrößen, versagt die Stütze. Diesen Zustand stellt die äußere Linie dar.

Bei gedrungenen Stützen sind die auftretenden Verformungen und damit die zusätzlichen Momente vergleichsweise gering. Die Stütze versagt durch Erreichen der Bruchschnittgrößen (Linie a). Bei mäßig schlanken Stützen nehmen die Verformungen und damit die Zusatzschnittgrößen nach Theorie II. Ordnung zu, so dass die aufnehmbare Normalkraft abnimmt. Die Stütze versagt jedoch noch durch Erreichen der Bruchschnittgrößen (Linie b). Da die Verformungen einen Einfluss auf die aufnehmbare Normalkraft haben, spricht man hier von einem Spannungsproblem nach Theorie II. Ordnung. Wird die Schlankheit noch weiter vergrößert, nehmen die Verformungen sehr stark zu, die Stütze wird instabil. Das äußere Moment wächst schneller als das aufnehmbare innere Moment, dadurch tritt Versagen ein, ohne dass der Stützenquerschnitt die Bruchschnittgrößen erreicht hat (Linie c). Deshalb spricht man hier von einem Stabilitätsversagen.

Für den theoretischen Fall des Stabilitätsversagens bei linear-elastischem Werkstoffverhalten kann die Knicklast mathematisch exakt nach Gleichung (5.1) bestimmt werden. Demnach ist die maximal aufnehmbare Last lediglich von der Biegesteifigkeit EI und der Knicklänge h_ef abhängig. Diese Beziehung wurde als erstes von Leonhard Euler erkannt, der für vier statische Systeme – den sogenannten Eulerfällen – die Knicklängen bestimmt hat.

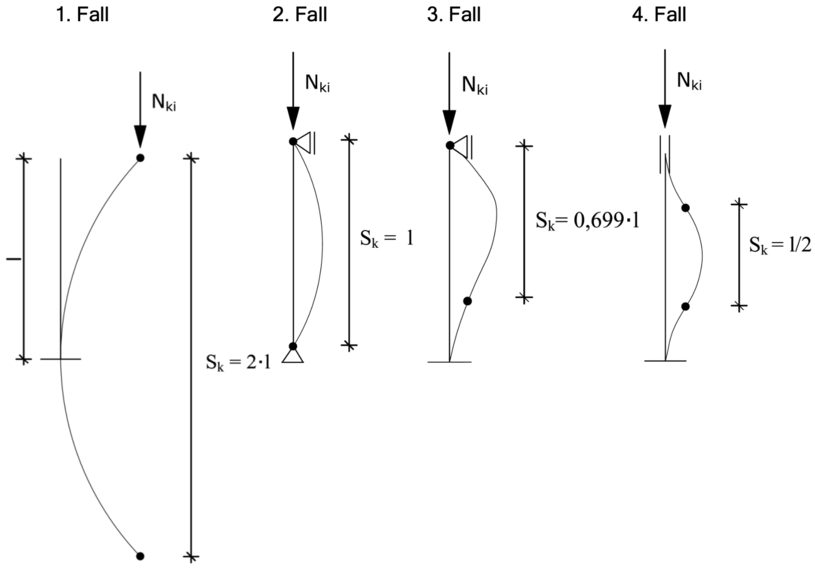
In Bild 5-2 sind diese vier Systeme dargestellt, wobei für die Knicklänge und die kritische Knicklast mit s_k bzw. N_ki die veralteten Bezeichnungen verwendet wurden.

mit

N_cr   kritische Knicklast
E_I     Biegesteifigkeit
h_ef   Knicklänge

Die theoretische Knicklast ist somit ausschließlich von den geometrischen Größen des betrachteten Bauteils abhängig. Die Knicklänge wird dabei aus dem Produkt eines Knicklängenbeiwerts ρ und der Systemlänge h bestimmt. Geometrisch gesehen entspricht die Knicklänge genau dem Abstand der Wendepunkte bei Betrachtung der Biegelinie des verformten Systems und stellt ein wesentliches Merkmal bei der Modellierung des Tragverhaltens schlanker Mauerwerkswände dar. Dies gilt auch bei Berücksichtigung eines wirklichkeitsnahen nichtlinearen Spannungs-Dehnungs-Verhaltens.

Aus diesen theoretischen Überlegungen kann für Mauerwerkswände abgeleitet werden, dass die Knickgefahr mit der Vergrößerung der Wandschlankheit λ = h / t anwächst bzw. die zugehörige Traglast entsprechend abnimmt. Auch bei großen Auflasten ist die Gefahr des Knickens deutlich erhöht. Des Weiteren haben die Lagerungsbedingungen der Wände insbesondere an den Wand-Decken-Knoten einen entscheidenden Einfluss darauf, wie groß die Knicklänge ist und damit ob die Wand als knickgefährdet zu betrachten ist oder nicht.