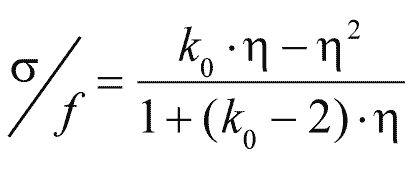2.3 Formänderungen von Mauerwerk
Skript PDF Download871 KB
2.3.2 Kennwerte
Bei Mauerwerk hängt das Last-Verformungs-Verhalten maßgeblich von der gewählten Mauerstein-Mörtel-Kombination ab. Trotz der großen Vielfalt möglicher Kombinationen und der zugehörigen Spannungs-Dehnungs-Beziehungen kann bei der Bemessung nach DIN EN 1996/NA vereinfachend von einem starr-plastischen Materialverhalten für alle Stein- und Mörtelarten ausgegangen werden. Bei verformungsabhängigen Nachweisen wird der Elastizitätsmodul als bestimmende Materialkenngröße nachweisbezogen (Knicksicherheitsnachweis oder Gebrauchstauglichkeitsnachweis) abgeschätzt.
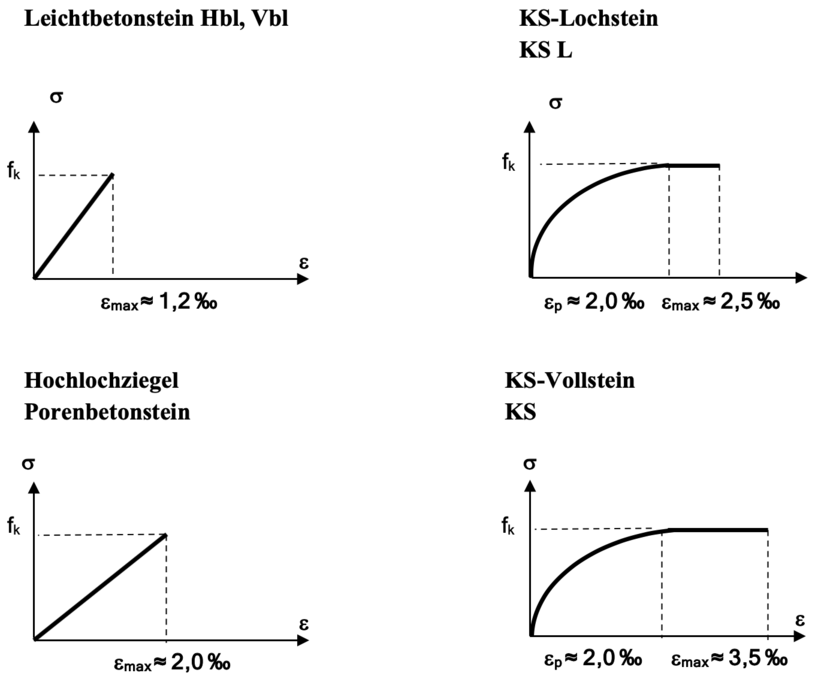
Das häufig nichtlineare Formänderungsverhalten von Mauerwerk war in den letzten Jahrzehnten Inhalt zahlreicher Forschungsvorhaben. Beispielhaft ist in Bild 2-7 ein Vorschlag für verschiedene Spannungs-Dehnungs-Beziehungen nach Schubert [18] dargestellt.
In Anlehnung an [7] können nach [11] die verschiedenen Formen der Spannungs-Dehnungs-Beziehung sehr realitätsnah über eine normierte mathematische Beziehung beschrieben werden.
Mit Hilfe dieser Formulierung kann eine beliebige nichtlineare Arbeitslinie zwischen den Grenzfällen linear-elastisch und starr-plastisch abgebildet werden. Dabei wird die Völligkeit der Spannungs-Dehnungs-Beziehung sowohl für 0 ≤ η ≤ 1 als auch der Verlauf der abfallenden Spannungen η > 1 allein mit Hilfe des bezogenen Ursprungsmoduls k0 = Ep∙ε0/fk festgelegt. Diese Kennzahl liegt bei Ziegel oder Porenbetonmauerwerk in der Größenordnung von 1,1 bis 1,5, während sie für KS-Mauerwerk etwa 1,8 bis 2,5 beträgt. Der Eurocode 6 enthält weitere in Tabelle 2-5 angegebene Verformungskennwerte für verschiedene Mauerwerksarten.
Tabelle 2-5: Verformungskennwerte von Mauerwerk nach [8]
| Mauersteinart | Mauermörtelart | Endkriechzahl a φ ∞ | Endwert der Feuchtedehnung b mm/m | Wärmeausdehnungs-koeffizient αt 10-6 / K | E-Modul N/mm2 | ||||
| Rechenwert | Wertebereich | Rechenwert | Wertebereich | Rechenwert | Wertebereich | Rechenwert | Wertebereich | ||
| Ziegel | Normalmauermörtel / Dünnbettmörtel | 1,0 | 0,5 – 1,5 | 0 | -0,1 c – +0,3 | 6 | 5 – 7 | 1100 · fk | 950 – 1250 · fk |
| Leichtmauermörtel | 2,0 | 1,0 – 3,0 | |||||||
| Kalksandstein | Normalmauermörtel / Dünnbettmörtel | 1,5 | 1,0 – 2,0 | -0,2 | -0,3 – ‑0,1 | 8 | 7 – 9 | 950 · fk | 800 – 1250 · fk |
| Betonsteine | Normalmauermörtel | 1,0 | - | -0,2 | -0,3 – ‑0,1 | 10 | 8 – 12 | 2400 · fk | 2050 – 2700 · fk |
| Leichtbetonsteine | Normalmauermörtel | 2,0 | 1,5 – 2,5 | -0,4 | -0,6 – ‑0,2 | 10; 8 d | 950 · fk | 800 - 1100 · fk | |
| Leichtmauermörtel | -0,5 | -0,6 – ‑0,3 | |||||||
| Porenbetonsteine | Dünnbettmörtel | 0,5 | 0,2 – 0,7 | -0,1 | -0,2 – +0,1 | 8 | 7 – 9 | 550 · fk | 500 – 650 · fk |
| a Endkriechzahl φ∞ = ε∞ / εel, mit εc∞ als Endkriechmaß und εel = σ/E. b Endwert der Feuchtedehnung ist bei Stauchung negativ und bei Dehnung positiv angegeben. c Für Mauersteine < 2 DF gilt der Grenzwert – 0,2 mm/m. d Für Leichtbeton mit überwiegend Blähton als Zuschlag. | |||||||||