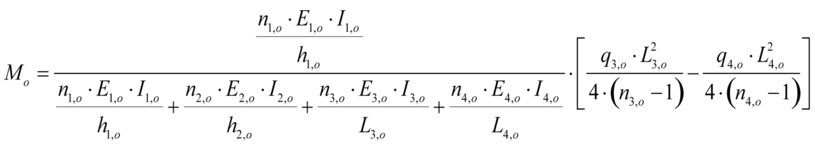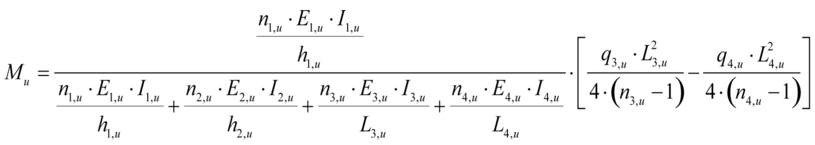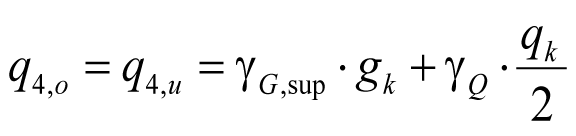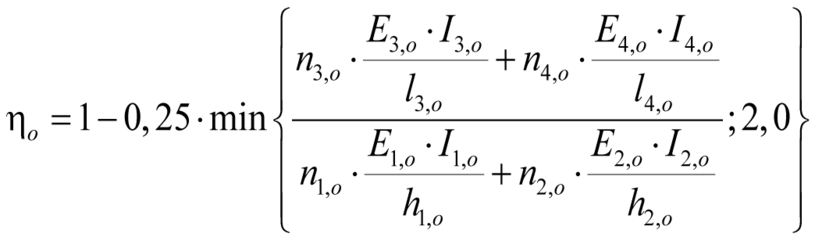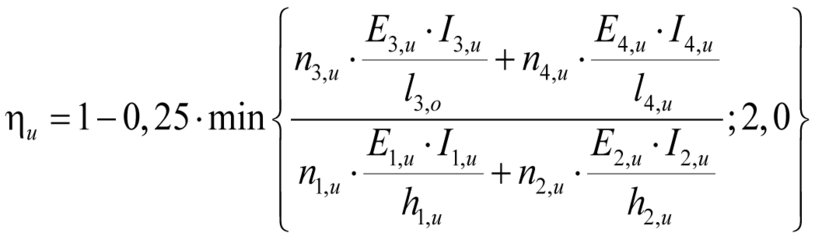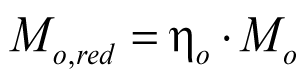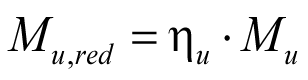7 - Bemessung von unbewehrtem Mauerwerk für Normalkraft- und Biegebeanspruchung nach dem allgemeinen Nachweisverfahren
Skript PDF Download752 KB
7.2 Bestimmung der Knotenmomente
Für die Berechnung der Traglastfaktoren werden im allgemeinen Berechnungsverfahren die Knotenmomente am Wandkopf und Wandfuß benötigt. Die sich aus der Deckenbelastung ergebenden Auflagerkräfte sowie die Eigenlasten des Mauerwerks dürfen wie im vereinfachten Verfahren nach Kap. 4.2.1 ermittelt werden. Die Stahlbetondecken können sich im Auflagerbereich - insbesondere bei darüber stehenden Wänden - jedoch nicht frei verdrehen, so dass Einspannmomente zwischen Decke und Wand entstehen. Während in der Stahlbetondecke diese Momente in der Regel durch Bewehrung konstruktiv abgedeckt werden, sind sie bei der Wandbemessung nach dem allgemeinen Verfahren explizit zu berücksichtigen. Dies bedeutet, dass bei Außenwänden mit einseitiger Wandauflagerung und bei Zwischenwänden mit unterschiedlicher angrenzender Deckenstützweite die Vertikallasten mit einer planmäßigen Exzentrizität e = MEd/NEd angreifen. Zur Anwendung kommen die Bemessungswerte der Einwirkungen. Für eine genauere Bestimmung der an Wandkopf und Wandfuß angreifenden Biegemomente aus Deckeneinspannung wäre bei mehrgeschossigen Gebäuden eine Rahmenberechnung unter Ansatz der tatsächlichen Biegesteifigkeiten von Wänden und Decken erforderlich. Da jedoch ein derartiges Vorgehen wegen unterschiedlicher Auswirkungen der Rissbildung in den einzelnen Bauteilen die wirklichen Verhältnisse nur bedingt wiedergibt und eine nicht vorhandene Genauigkeit vortäuscht, ist es in den meisten baupraktischen Fällen mit hinreichender Gebäudeaussteifung sinnvoll, für die Ermittlung der Knotenmomente lediglich ein Teilsystem zu betrachten.
Zur Bestimmung der Knotenmomente stehen verschiedenen Rechenverfahren zur Verfügung. Neben dem in Anhang C von DIN EN 1996-1-1/NA angegebenen Verfahren existiert ein Näherungsverfahren nach Cross und Kani (sogenannte Cross-Kani-Verfahren). Im Folgenden soll hier nur auf das Verfahren nach DIN EN 1996-1-1/NA Anhang C eingegangen werden.
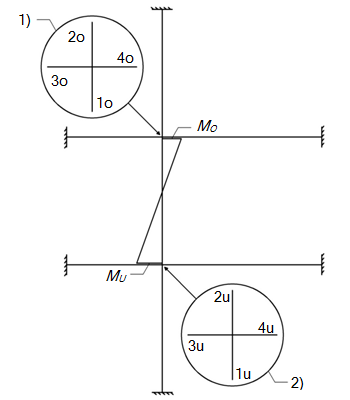
Die Berechnung der am Wandkopf oder Wandfuß auftretenden Biegemomente Mi kann vereinfacht entsprechend Bild 7-1 erfolgen. Hierzu werden die Schnittkräfte an einem Wand-Decken-Knoten ermittelt, der aus der Decke mit den ober- und unterhalb anschließenden Wänden gebildet und als Teil eines Rahmensystems betrachtet wird. Die Deckenlänge reicht hierbei bis zum Nachbarknoten, die Wandabschnitte über die Höhe der Wand und die Stabenden werden als eingespannt oder frei gelagert definiert. Die vom Knoten abliegenden Stabenden sollten daher als eingespannt modelliert werden, wenn diese in der Lage sind, Biegemomente aufzunehmen. Anderenfalls sind sie als gelenkig gelagert zu betrachten.
Für die Bemessung des Innenwandknotens – insbesondere am Wand-Decken-Knoten der 1. Innenwand – kann es in besonderen Fällen sinnvoll sein, am benachbarten Außenwandknoten mit geringer einwirkender Normalkraft (z.B. Außenwand im obersten Geschoss) eine gelenkige Deckenauflagerung im Teilsystem anzunehmen. Dies führt zu größeren Deckeneinspannmomenten im betrachteten Knoten und damit gegebenenfalls zu größeren Ausmitten der Deckenauflagerkraft.
Der Tragwerkplaner muss daher abwägen, welches Teilsystem der statischen Berechnung sinnvoll zugrunde gelegt werden kann. Zur Festlegung kann es zweckmäßig sein, unterschiedliche Teilsysteme zu untersuchen. Die Stabendmomente Mo am Wandkopf und Mu am Wandfuß können mit den Gleichungen (7.2) und (7.3) berechnet werden.
mit
ni Steifigkeitsfaktor des betrachten Stabes i
n = 3 bei eingespannten Stäben am abliegenden Ende (z.B. Außenwand)
n = 4 bei gelenkiger Lagerung am abliegenden Ende (z.B. Innenwand)
Ei Elastizitätsmodul des betrachteten Stabes i
Ii Trägheitsmoment des betrachteten Stabes i Bei zweischaligem Mauerwerk mit Luftschicht, bei dem nur eine Wandschale belastet ist, darf für Ii nur das Trägheitsmoment der belasteten Wandschale angenommen werden. In den meisten Fällen sind die wirksame Breite der Decke und die Breite der Wand gleich groß, d. h. es gilt bB/bD = 1. Bei Anordnung von Wandöffnungen oder Deckendurchbrüchen in Randnähe können die Breiten von Decke und Wand unterschiedlich sein.
Bei teilaufliegender Decke darf bei der Berechnung der Flächenträgheitsmomente der angrenzenden Wände die Auflagertiefe anstelle der vollen Wanddicke angesetzt werden, jedoch mindestens die halbe Wanddicke (t = a ≥ t/2), siehe Kap. 7.3
h1 lichte Höhe des Stabes 1
h2 lichte Höhe des Stabes 2
l3 lichte Spannweite des Stabes 3 (längeres Deckenfeld)
l4 lichte Spannweite des Stabes 4 (kürzeres Deckenfeld)
q3 die gleichmäßig verteilte Bemessungslast des Stabes 3 bei Anwendung der Teilsicherheitsbeiwerte für ungünstige Einwirkung nach Gleichung (7.4)
q4 die gleichmäßig verteilte Bemessungslast des Stabes 4 bei Anwendung der Teilsicherheitsbeiwerte für ungünstige Einwirkung nach Gleichung (7.5)
o, u Fußzeiger Wandkopf und Wandfuß
Die anzusetzenden Bemessungslasten auf den Decken werden nach den Gleichungen (7.4) und (7.5) bestimmt.
Bemessungslast auf dem längeren Deckenfeld:
Bemessungslast auf dem kürzeren Deckenfeld:
Die sich nach Gleichung (7.2) und Gleichung (7.3) ergebenden Knotenmomente Mo und Mu dürfen aufgrund der Verträglichkeitsproblematik und der daraus resultierenden rechnerischen Rissbildung in Wand und Decke mit dem Faktor ηo nach Gleichung (7.6) (bzw. ηu mit Gleichung (7.7)) reduziert werden.
mit
ni Steifigkeitsfaktor des betrachten Stabes i
n = 3 bei eingespannten Stäben am abliegenden Ende (z.B. Außenwand)
n = 4 bei gelenkiger Lagerung am abliegenden Ende (z.B. Innenwand)
Ei Elastizitätsmodul des betrachteten Stabes i
Ii Trägheitsmoment des betrachteten Stabes i Bei zweischaligem Mauerwerk mit Luftschicht, bei dem nur eine Wandschale belastet ist, darf für Ii nur das Trägheitsmoment der belasteten Wandschale angenommen werden. In den meisten Fällen sind die wirksame Breite der Decke und die Breite der Wand gleich groß, d. h. es gilt bB/bD = 1. Bei Anordnung von Wandöffnungen oder Deckendurchbrüchen in Randnähe können die Breiten von Decke und Wand unterschiedlich sein.
h1 lichte Höhe des Stabes 1
h2 lichte Höhe des Stabes 2
l3 lichte Spannweite des Stabes 3
l4 lichte Spannweite des Stabes 4
o, u Fußzeiger Wandkopf und Wandfuß
Die für die Bemessung zugrunde zu legenden Biegemomente lauten somit:
mit
ηo Faktor zur Abminderung des Knotenmomentes am Wandkopf nach Gleichung (7.6)
ηu Faktor zur Abminderung des Knotenmomentes am Wandkopf nach Gleichung (7.7)
Mo Bemessungswert des Knotenmomentes am Wandkopf nach Gleichung (7.2)
Mu Bemessungswert des Knotenmomentes am Wandfuß nach Gleichung (7.3)
o, u Fußzeiger Wandkopf und Wandfuß