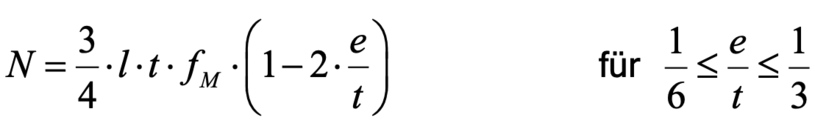2 - Festigkeits- und Verformungseigenschaften
Skript PDF Download871 KB
2.1 Grundlagen der Spannungsverteilung im Mauerwerk
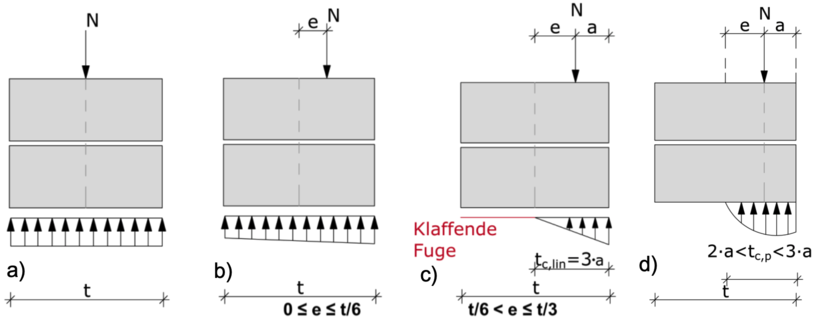
Der Werkstoff Mauerwerk eignet sich in hervorragender Weise zur Abtragung von Vertikalkräften, da diese in der Wand überwiegend Druckspannungen hervorrufen. Sie werden im Allgemeinen zunächst zentrisch eingeleitet und erzeugen so eine konstante Spannungsverteilung im Querschnitt (s. Bild 2-1 (a)). Infolge einer exzentrischen Lasteinleitung am Wandkopf bzw. Wandfuß, aber auch infolge von Imperfektionen bei der Herstellung, tritt im Querschnitt zusätzlich eine Momentenbeanspruchung auf, die einen nicht vernachlässigbaren Einfluss auf die Spannungsverteilung hat. Je nach Größe der Lastexzentrizität ergeben sich unterschiedliche Spannungsverläufe.
Ist bei Annahme linear-elastischen Materialverhaltens die Ausmitte kleiner als ein Sechstel der Wanddicke, resultiert eine annähernd lineare Spannungsverteilung mit überdrücktem Querschnitt (s. Bild 2-1 (b)). Bei größerer Ausmitte (e/t > 1/6) bildet sich eine klaffende Fuge, da im Mauerwerksbau keine nennenswerten Zugspannungen senkrecht zur Lagerfuge aufgenommen werden können. Die Spannungsverteilung ist im überdrückten Bereich dann dreiecksförmig, wie in Bild 2-1 (c) dargestellt. Bei realistischer Berücksichtigung des nichtlinearen Werkstoffverhaltens von Mauerwerk nehmen die Druckspannungen bei größeren Ausmitten jedoch überproportional zu, woraus sich eine völligere Druckspannungsverteilung ergibt (s. Bild 2-1 (d)).
Für den Fall einer linearen Spannungsverteilung kann die aufnehmbare Normalkraft in Abhängigkeit der vorhandenen Lastexzentrizität nach den Gleichungen (2.1) und (2.2) berechnet werden.
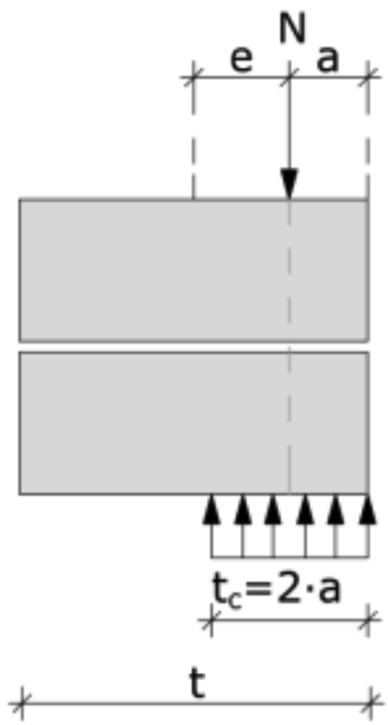
Nach DIN EN 1996-1-1/NA darf für Mauerwerk aus künstlichen Steinen für alle Nachweise im Grenzzustand der Tragfähigkeit vereinfachend von starr-plastischem Werkstoffverhalten und gerissenem Querschnitt ausgegangen werden. Damit vereinfacht sich die Spannungsverteilung zu einem konstanten Spannungsblock, der nur über eine begrenzte Breite des Querschnitts wirkt (s. Bild 2-2). Die aufnehmbare Normalkraft berechnet sich hierfür in Abhängigkeit der Exzentrizität wie folgt:
mit
e/t Verhältnis Lastexzentrizität zu Wanddicke (e/t = M/(N∙t))
M Biegemoment (am betrachteten Wandquerschnitt)
N Normalkraft (am betrachteten Wandquerschnitt)
l Wandlänge
fM Mauerwerksdruckfestigkeit